 De vegades se m’acudeixen idees per plantejar aquí que presenten una dificultat afegida, i és que algú ja ho ha expressat d’una manera magistral. Podria posar el link i prou, però em costa resistir la temptació de tornar a insistir en algun tema. I això és el que em passa amb un dels articles que més m’han impactat. L’autor va ser l’Stephen Jay Gould, que el va titular “La mediana no és el missatge” i hi ha una traducció al castellà aquí.
De vegades se m’acudeixen idees per plantejar aquí que presenten una dificultat afegida, i és que algú ja ho ha expressat d’una manera magistral. Podria posar el link i prou, però em costa resistir la temptació de tornar a insistir en algun tema. I això és el que em passa amb un dels articles que més m’han impactat. L’autor va ser l’Stephen Jay Gould, que el va titular “La mediana no és el missatge” i hi ha una traducció al castellà aquí. El cas és que la ciència és una activitat que associem indefectiblement a càlculs exactes, a respostes precises i a problemes resolts. Això és una percepció errònia, i la realitat dels científics és justament la contraria: enfrontar-se a problemes poc clars, amb dades dubtoses i resultats contradictoris. Però en l’imaginari popular, quan un científic dona una dada, aquesta va a missa.
I això és un problema si la dada és estadística, perquè les interpretacions d’aquesta mena de dades estan carregades de subtileses i matisos. I per acabar d’arrodonir-ho, tenim molts estereotips profundament inculcats en la nostra ment que encara tergiversen mes les coses.
Hi ha una situació particularment dramàtica en què això és posa de manifest. I això és el que li va passar a en Jay Gould. El metge li va comunicar que patia un mesotelioma abdominal. Un tipus de càncer particularment agressiu. Quan va buscar informació va trobar la dada demolidora: L’esperança de vida en aquell tipus de càncer és de tant sols 8 mesos.
És una escena que l’hem vist en mil pel·lícules. El metge informa al pacient del diagnòstic. Càncer. Moments després el pacient fa la pregunta: Quant de temps em queda? I el metge, amb posat seriós dona un nombre determinat de mesos.
Tots ho hem vist, però aquesta situació simplement no és real.
Els metges saben prou bé que els càncers són molt variables, que els 8 mesos aquells són un valor medi, però que la variabilitat pot ser molt gran i, per tant, mai diuen “li queda tant temps de vida”. Però tant se val. En la conversa sortirà la xifra estadística i en la ment del pacient s’interpretarà “M’ha dit que em queden 8 mesos”.
Com que són moments molt dramàtics és comprensible. Però si fem un exemple diferent ens adonem de l’error. L’alçada mitja de la població masculina pot ser d'un metre setanta-cinc, però ningú espera mesurar exactament això pel simple fet de ser home. Sabem que hi ha una variació important. Doncs amb les dades sobre la supervivència del càncer (i de totes les malalties) passa exactament el mateix.
Les coses són complexes, les malalties no sempre són previsibles. Cada persona és un món. I això fa que calgui interpretar les dades amb fredor. Fa poc una famosa cantant va morir de càncer de pàncrees. L’esperança de vida en aquest cas és de poc més de cinc mesos, però ella va viure dos anys després del diagnòstic. Potser perquè va anar a Houston a operar-se? Doncs segurament no. El tractament que s’aplica aquí i allà és el mateix. Però els cinc mesos sols són una mediana. Hi ha pacients que viuen cinc anys i no és cap miracle (ni cap efecte de la dieta energètica del curandero de torn). Simplement va tenir la sort d’estar al costat dret de la corba de supervivència.
I finalment, també hi intervé l’actitud personal, l’estat anímic. Deixar-se enfonsar per una dada mal interpretada pot afavorir el progrés de la malaltia. Tots sabem que hi ha "un temps per viure i un per morir", però això no implica deixar de lluitar per retardar el moment inevitable de la mort. Desprès de tot les dades sols s’apliquen a un moment determinat. Potser el mes que ve apareixerà un nou fàrmac que ho canviarà tot.
Quan reflexiones sobre la malaltia, la mort, la manera d’afrontar-ho, difícilment trobes respostes clares. Tant sols puc fer el joc d’ajuntar dues frases tretes de contextos diferents però que juntes generen un plantejament que, a mi, em reconforta. La primera és la que li va dir Isaïes a Ezequies per algun lloc de la Bíblia (Reis, 20), i la segona és del gran Miquel Martí i Pol.
“Posa la teva casa en ordre, perquè moriràs i no viuràs... I en acabat que cadascú es vesteixi com bonament li plagui, i via fora!, que tot està per fer i tot és possible".













9 comentaris :
Ara que dius això, recomano un llibre que es diu "Sobre el duelo y el dolor". Per a persones que la vida, actualment, no s'està portant massa bé.
Dan, crec que jo no voldria saber el temps que em queda. Simplement viure cada minut intensament.
Aqui està la cosa. En realitat, no podem saber quan temps queda. Tant sols aproximacions que cal pendre amb pinces. Però, si, cal aprofitar tots i cada un dels minuts a tope.
QUe faries abans de morir?
Sincerament no en tinc ni idea. Pero sospito que res del que pugui pensar ara seria el que faria a l'hora de la veritat.
En tot cas, anirem fent de manera que quan sigui el moment ja quedin poques coses pendents!!
La pregunta de la txell és bona. una vegada, a l'Asimov, li van preguntar:
- quàn es cansarà d'escriure?
- Dons quen em mori.
- I quàn es morirà
- Mai!
- I què faria si li diguessin que li queda un mes de vida?
- Doncs escriuria més ràpid ...
Tot un personate.
Una pregunta Dan. Si tan poc sabem d'aquest tipus de càncer, per què els metges no ens diuen la veritat com ho has fet tú?
Salut!
Omalaled, jo crec que els metges en general la diuen la veritat. Altra cosa es que els entenguem o que interpretem correctament el que diuen.
be, però en fer la mediana ja s'ha de tenir en compte que els valors extrems no tindran quasi influència en el valor obtingut. Potser en comptes de la mediana es podria fer la mitjana, allò tan simple de sumar tots els valors i dividir-lo pel nombre de valors i, així, els valors extrems tindrien més influència. Però be, l'estadística és estadística. Un profe meu sempre deia que si ell es menja un pollastre i jo me'l miro, l'estadística dirà que ens hem menjat mig pollastre cadascú. Una analogia massa rustica però amb un cert punt de raó: l'estadística és una molt bona orientadora, però sempre hi pot haver excepcions.
Si la mediana surt que l'esperança de vida de cert càncer és de 8 mesos doncs no vol dir que s'hagi de viure 8 mesos, però si que 8 mesos és el valor en mig (que no mitjà) de tota la sèrie de valors de que se'n disposa. Així hi haurà tanta gent que hagi mort abans dels 8 mesos com després, tot i que els que han mort abans dels 8 mesos igual ho han fet tots entre el setè i el vuitè mes, metre que els que han mort després dels 8 mesos ho han fet tots, per exemple, a partir dels 12 mesos. La mediana, aleshores, s'allunya molt de la mitjana! (variança es deia, oi? no se, fa massa temps que vaig fer probabilitat i estadística i val a dir q no em molava massa)
Total, he deixat anar un rotllo per dir que si, que cada cas és un món, però que les estadístiques (si estan ben fetes) són una bona guia.
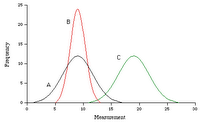
Si, en quasi tot, Pero estas asumint que la corva de supervivencia te forma de campana de gauss. I no sempre es així! Pot tenir una cua molt llarga a la dreta, pero per l'esquerra hi ha un limit temporal que es el moment del diagnostic. Aleshores, la mitjana i la mediana poden variar molt. Segons el tipus de cancer, el la supervivencia promig pot ser molt curta, pero alguns casos viure molts anys, si la cua de la distribució s'allarga molt.
Buf, quin rotllo estadistic, pero el missatge final es que no es pot agafar una dada simplement i considerar-la una mena de sentencia.
L'estadística mai menteix menteix qui l'interpreta, que habitualment no és ni estadístic ni matemàtic, sinó algú que la fa servir d'escut per demostrar les seves hipòtesis. L'escriptor de la màquina del temps, HG Wells, va dir que un dia el raonament estadístic seria tan important per a ser un bon ciutadà com el llegir i l’escriure.
Publica un comentari a l'entrada